
1.罪犯困境(非零和博弈典型)
这是本游戏的底子博弈模型,对此最经典的论述为:
两个嫌疑犯作案后被差人抓住,分别关在不同的屋子里接受审问。
差人知道两人有罪,但短少满足的根据。差人通知每个人:如果两人都狡赖,各判刑一年;如果两人都招供,各判八年;如果两人中一个招供而另一个狡赖,率直的放出去,狡赖的判十年。
于是,每个罪犯都面临两种选择:招供或狡赖。可是,不管同伙选择什么,每个罪犯的最优选择是招供:如果同伙狡赖、自己招供的话放出去,狡赖的话判一年,招供比不招供好;如果同伙招供、自己也招供的话判八年,比起狡赖的判十年,招供仍是比狡赖的好。
效果,两个嫌疑犯都选择招供,各判刑八年。
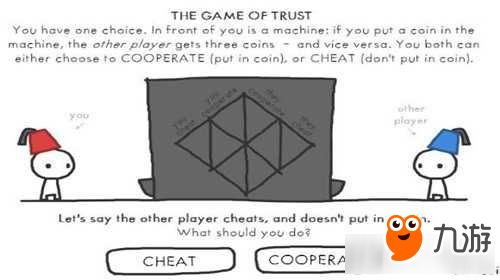
就像这个游戏机一样,当你投一个硬币进去,对方就会得到两枚硬币。显着,关于全体来说,选择协作得到的报答最高(每人失掉1个,得到2个,总和添加2个),但对个人而言风险也是最大的(对方选择欺诈,你-1,对方3,总和2),所以在这种形势下,欺诈变成了最优战略。这样的形势,归根到底,是由于两头短少交流而导致的。在无法信任对手的一局游戏中,欺诈师往往会成为毕竟的赢家。有意思的是,罪犯困境推广到判定的N局游戏中也是树立的。
原因如下:
关于第N局,由于不用忧虑之后被报复(毕竟一局了嘛),最优战略显着是欺诈。
关于第N-1局,由于现已知道了对方下一局的最优战略是欺诈,为了防止遭到更多丢失,最优战略显着也是欺诈。
关于第N-2局,……
所以,关于判定的N局游戏,最优战略永远是欺诈。
2.重复困境
这个升级版的罪犯困境源于一个全世界的重复罪犯困境竞赛(也是这个游戏的来历)。
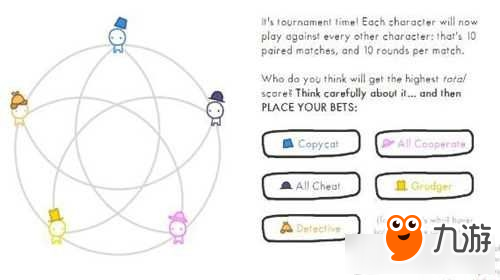
在这个竞赛中,许多博弈论专家将自己的战略编写成程序,和其它程序进行博弈(没错,游戏里的战略是其间的一些)
通过许多许多轮竞赛后,出乎意料的是,最佳判定性战略被认为是“以眼还眼”,这是阿纳托尔·拉波波特(Anatol Rapoport,《协作的进化》作者,也是竞赛的发起人)开发并运用到锦标赛中的办法。
这个战略只不过是在博弈的开始选择协作,然后,采纳对手前一回合的战略。
在完美的博弈中,Copycat(小蓝人,顺从者)是最有用的。这种战略较好地规避了被欺诈的风险(被骗了仍是要涨点回忆),而关于协作者,显着两头都能获得较高的获利。
而关于有可能失误的博弈(玩家预备协作,可是由于各种不可控要素构成变节的效果),更好些的战略是“宽恕地以眼还眼”,即当你的对手变节,鄙人一回合中你无论如何要以小概率(大约是1%~5%)时而协作一下。这是考虑到偶尔要从循环变节的上傍边康复。毕竟,博弈学家核算全部战略得到这样一个结论:最好的战略满足四个要素:友善,报复,宽恕,不嫉妒。
简略来说,发表协作的意向(让潜在的协作者与你协作),不盲目乐观(防止一贯被欺诈师欺诈),恰当包容小的失误(防止因误会导致的彼此不信任),不寻求比对手更高的得分(更高意味着恶性竞争)。
因此,一些学者们据此得到一种给人以乌托邦形象的结论,认为自私的个人为了其自私的利益会趋向友善、宽恕和不嫉妒,即人人为我的社会可能树立在对利益的寻求上。事实上,罪犯困境并不是那么简略,Copycat也并不总是毕竟的赢家。
在短期博弈上,最有用的往往是欺诈。

在变节的报答更高时,欺诈往往能获得毕竟成功。
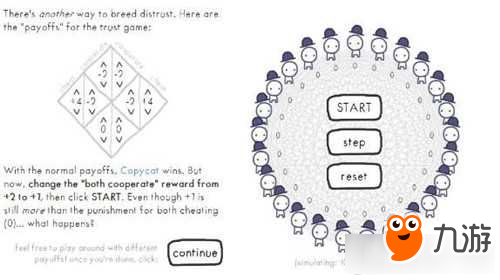
在失误率过高时,效果趋于混沌。

声明:九游网登载此文出于传递信息之目的,不代表九游网赞同其观点或证实其描述,若侵权请来信告知,我们将及时处理。
看了上边这篇信任的进化怎么玩,各位玩家是否都了解相关信息了呢!找精彩好玩手机游戏请浏览九游。













文章评论